반달가면 이글루에서 백업 - http://bahndal.egloos.com/638108 (2020.5.15)
월터 미베인(Walter R. Mebane Jr.) 교수의 논문은 아래의 링크에서 받을 수 있다.
Anomalies and Frauds in the Korea 2020 Parliamentary Election - Walter R. Mebane, Jr.
(현재 시점에서는 해당 파일이 홈페이지에서 내려간 듯 하다. 따라서 pdf 파일을 여기에 첨부한다)
내가 통계학 전공자도 아닌지라, 논문 내용 전체에 대해 종합적으로 얘기하긴 어렵고 전반부에 제시된 그래프에 관하여 정성적으로 이해한 내용에 대해서만 정리해 보려고 한다. (점심 시간을 쪼개 가면서 논문을 읽다니, 대학원 다닐 때도 안 하던 짓을 하고 말았다. -_-;)
우선 아래의 문제를 생각해 보자. 인문계열에겐 조금 어려울 수도 있겠다. 양해를 구한다.
1) 어느 초등학교의 5학년 학생이 모두 1000명이다. 이번에 치른 교내 산수시험 점수의 분포는 어떻게 될까?
가. 가우스 분포(정규 분포)
나. 알 수 없다.
다. 기타 ( )
2) 작년 2학기에 전국의 중학교 3000개에서 치렀던 2학년 반장선거를 조사해 보았다. 각 학급별 당선자의 득표율(%)을 전부 모았다. 이 득표율의 분포는 어떻게 될까?
가. 가우스 분포(정규 분포)
나. 알 수 없다.
다. 기타 ( )
3) 인구 5천만명인 어느 국가의 국회의원 선거에서 전국의 각 투표소별로 1위 득표후보의 득표율을 전부 조사해서 모았다. 투표소는 총 1만5천개소다. 득표율의 분포는 어떻게 될까?
가. 가우스 분포(정규 분포)
나. 알 수 없다.
다. 기타 ( )
4) 인구 5천만명인 어느 국가의 국회의원 선거에서 전국의 각 투표소별로 투표율을 전부 조사해서 모았다. 투표소는 총 1만5천개소다. 투표율의 분포는 어떻게 될까?
가. 가우스 분포(정규 분포)
나. 알 수 없다.
다. 기타 ( )
5) 중심극한 정리(central-limit theorem)에 대하여 설명하라. (주관식)
어떤 집단에 대하여 관심이 있는 항목을 수치화하여 수집할 때 표본 규모가 충분히 크고 무작위성이 있다면 통상 가우스 분포(Gaussian distribution)를 보이게 된다. 우리가 통계적으로 관측/분석하는 자연과학/사회과학 현상에서 너무나 많이 나타나서 그런지 정규 분포(normal distribution)라고도 불린다. 정상적이고 평범한, "normal"한 분포라는 의미다. 가우스 분포는 종 모양의 곡선(bell-shaped curve)이면서 봉우리가 하나인 분포(unimodal distribution)다.
미베인 교수의 eforensics 모델은, 이러한 기본적인 전제에서 출발해서 단지 "분포 모양이 좀 이상하다"는 식의 정성적인 명제가 아니라 무엇 때문에 얼마나 이상한 것인지를 정량적으로 도출하기 위해 고안해 낸 통계적 분석 모델인 것으로 보인다. 이 모델 자체를 공부할 시간은 없으니, 여기서는 왜 미베인 교수가 조작 가능성이 높아 보인다는 판단을 내리게 되었는지에 대해 정성적이고 기초적인 고찰만 해 보고자 한다.
미베인 교수의 논문을 보면 그래프가 몇개 보이는데, 가로축은 투표율이고 세로축은 관심 대상의 득표율이다. 여기서 관심 대상은 민주당(Democratic Party) 또는 정당과 무관하게 1위 후보(constituency leader)다.

우선 논문의 Figure 1(a)를 살펴 보자. 가로축은 투표율(turnout proportion)이고 세로축은 민주당(Democratic Party) 득표율(proportion of leading votes)이다. 투표소별로 투표율과 득표율을 계산해서 점을 찍어 놓은 형태인데, 2개의 군집으로 나뉜 것을 볼 수 있다.
중간 하단에 이루어진 군집은 당일투표이고, 투표율(가로축)이 1.00, 즉 100%에 근접한 부분에 길쭉하게 이루어진 군집이 사전투표이다. 사전투표가 이렇게 투표율 100%쪽으로 몰린 이유는 사전투표를 미리 신청하는 형식이 아니었기 때문에 선관위에서 그냥 사전투표에 나타난 사람 수를 사전투표 유권자수로 간주하여 데이터셋을 구성했기 때문이다. 모두가 100%가 아닌 이유는 기권표 때문에 90%대로 떨어진 부분들이 있는 것으로 보인다.
Figure 1(a)의 투표율(가로축) 히스토그램(histogram)을 보자. 당일투표 군집은 깔끔하게 단봉형 분포를 나타낸다. 사전투표 군집은 바로 앞에서 언급한 문제로 인해 투표율이 1.00에 몰려 있기 때문에 분석 측면에서 별 의미가 없다.
이제 Figure 1(a)의 민주당 득표율(세로축) 히스토그램을 보자. 가우스 분포에 가까운 것이 아니라 뭔가 좀 이상한 모양을 하고 있다. 여기서부터 일단 이 결과가 뭔가 자연스럽지 않다는 생각이 들게 된다. 내가 일을 하다가 저런 모양을 봤다면 혹시 데이터 입력에 문제가 있는지 다시 한번 확인해 볼 것이다.
Figure 1(b)도 같은 형식인데, 이번에는 세로축이 민주당 득표율이 아니라 정당 불문하고 당선후보(constituency leader)의 득표율이다. 히스토그램을 보면 마찬가지로 당일투표율(가로축)은 가우스 분포를 보이고 사전투표율은 1.00쪽에 붙어 있고 득표율(세로축)은 뭔가 좀 이상하다.
좀 더 자세히 나누어서 그래프를 그린 Figure 2로 넘어가 보자.
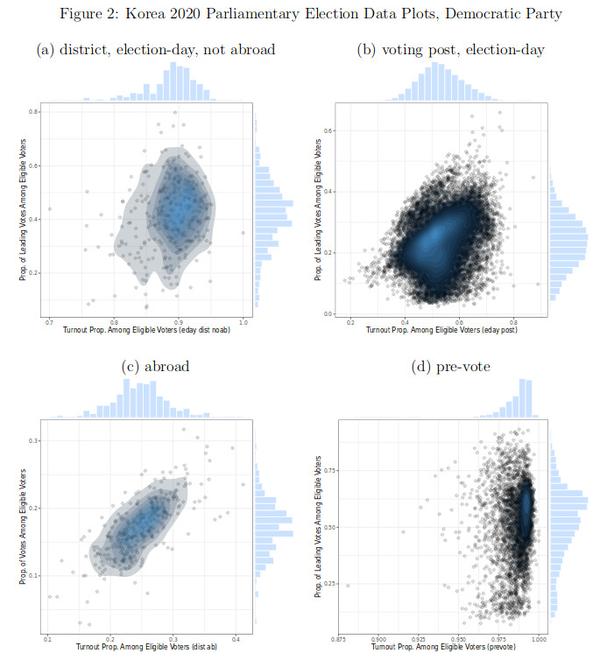
Figure 2는 민주당의 득표 상황을 분할해서 당일투표/사전투표/재외투표 등을 별도로 그래프를 그려 놓은 것이다.
Figure 2(a)는 투표소별이 아니라 선거구(district)별로 재외투표를 제외하고 투표율(가로축)과 민주당 득표율(세로축)을 그린 것이다. 가로축과 세로축 히스토그램 모두 가우스 분포가 아니라 뭔가 찌그러져 있다. 선거구별 재외투표는 Firgure 2(c)에 별도로 표시했는데 마찬가지로 히스토그램이 찌그러져 있다. 선거구의 수가 250여개로 상대적으로 적은데 히스토그램 구간은 촘촘하게 나누어서 들쭉날쭉해 보이는 것 같기도 하다.
Figure 2(b)는 투표소(voting-post)별 당일투표(election-day)에 대해서 투표율(가로축)과 민주당 득표율(세로축)을 나타낸 것이다. 가로축과 세로축 히스토그램 모두 가우스 분포에 근접하는 자연스러운 단봉형 분포다. 누구라도 수긍할 수 있는 정상적인 양상이다.
Figure 2(d)는 투표소별 사전투표(pre-vote)에 대해서 투표율(가로축)과 민주당 득표율(세로축)을 나타낸 것이다. 앞에서 이미 언급했듯이 가로축 히스토그램은 의미가 없고, 세로축 히스토그램을 봐야 한다. 가우스 분포가 아니라 찌그러져 있다. 아니, 찌그러진 정도가 아니라 아예 봉우리가 2개다.
Figure 3에 대한 설명은 생략하겠다. 당선후보 득표율을 가지고 그래프를 그린 것인데, 양상은 Figure 2와 비슷하다.
이후 후반부는 투표 결과가 얼마나 이상한가에 대해 확률을 계산하고 수치적으로 결과를 도출하는 내용인데, 복잡하기도 하고 잘 모르겠어서 일단 여기까지만 살펴보았다.
1만개가 넘는 투표소에서 1천만명이 넘는 유권자가 사전투표를 했다. 전국적으로 민주당 지지층에게 사전투표를 하라고 독려하고 통합당 지지층에게 사전투표에서 빠지라고 독려를 했다고 치자. 만약 실제로 민주당 지지층이 대거 사전투표로 몰려가고 통합당 지지층이 사전투표에서 빠졌다면, 사전투표에서 민주당 득표율이 올라갈 것이므로 Figure 2(d)의 세로축 히스토그램의 봉우리가 위쪽(민주당 득표율이 높은 수치쪽)으로 전이했을 것이다.
이러한 전이는 평균과 표준편차를 바꿀 수 있지만, 분포 자체는 가우스 분포여야 정상이다.
그런데 놀랍게도, 당일투표에서는 투표율과 득표율이 깔끔하게 가우스 분포를 나타내는데 사전투표의 득표율 분포는 통계적으로 볼 때 기적이라고 얘기할 만한 희한한 히스토그램을 보여주었다. 대체 사전투표에 참여한 1100만명은 대체 어떤 사람들이기에 지금까지 자연계와 인간계를 통틀어 그 누구도 이루지 못한 이런 놀라운 히스토그램을 이끌어낸 것인가?
만약 사전투표에서 민주당 지지층이 대거 몰려오고 통합당 지지층이 빠졌기 때문에 득표율 히스토그램에서 가우스 분포가 깨졌다고 가정해 보자. 그렇다면 당일투표에서 민주당 지지층이 대거 빠지고 통합당 지지층이 대거 몰려왔는데, 도대체 왜 당일투표 히스토그램은 그렇게 깔끔하게 가우스 분포를 유지하고 있는 것인가?
그럴수도 있다고? 지금 열명 스무명짜리 표본집단을 얘기하는 것이 아니다. 국가 전체를 아우르는 천만명 단위의 대규모 집단이다.
기술적인 측면에서 몇가지 원인을 상상해 볼 수 있겠다.
1. 미베인 교수가 당일투표 데이터 입력은 제대로 해서 깔끔한 가우스 분포가 나왔지만, 무슨 이유인지 사전투표 데이터 입력은 개판을 쳐서 입력 데이터 자체가 엉망이었다.
2. 미베인 교수의 데이터 입력엔 문제가 없었지만, 애초에 기초자료가 된 선관위의 데이터 집계에 뭔가 오류가 있다.
3. 미베인 교수의 데이터 입력에도 선관위 데이터 집계에도 오류가 없었고, 누군가 사전투표 자체를 조작했다.
4. 무려 1100만명에 달하는 사전투표 참가자들 대다수가 알 수 없는 어떤 초자연적인 영향으로 가우스 분포를 깨부수는 통계적 기적을 창출해 냈다. 통계적 기적을 창출할 가능성에 대한 문제는 이전 게시물을 참고하자. 여기로
5. 기타: (댓글이나 트랙백 대환영)
논문의 결론을 보면, 미베인 교수는 eforensics 모델로 검증했을 때 이번 국회의원 선거 데이터가 조작되었을 가능성이 농후하다고 판단하고 있다. 다만, 조작이 아니라 다른 영향(전략적 행동 등)에 의한 변이를 조작으로 판정할 가능성도 없지는 않다고 언급하고 있다. 대상 국가의 정치적/사회적 상황은 제외하고 오로지 수자들의 집합을 이용해서 해석한 결과이므로 당연히 조작을 100% 단정할 수는 없기 때문이다.
따라서, 이 논문의 결론은 "선거는 분명히 조작되었다"라기보다는 "개표결과가 매우 이상하여 조작 가능성이 상당히 농후해 보이므로, 반드시 조사하여 검증할 필요가 있다"로 해석되어야 한다. 논문의 마지막 부분을 여기에 다시 써 둔다.
Statistical findings such as are reported here should be followed up with additional information and further investigation into what happened. Most important, and in principle perhaps simplest to do, is to validate the paper ballots, and once they have been validated to count the paper ballots manually. The statistical findings alone cannot stand as definitive evidence about what happened in the election.
여기에 보고된 통계 결과와 관련하여, 무슨 일이 벌어졌는지에 대한 추가적인 조사와 정보공개가 뒤따라야 한다. 가장 중요한 일은 - 그리고 아마도 가장 간단한 일은 - 투표지의 유효성을 검증하고 사람 손으로 다시 개표하여 집계하는 것이다. 통계 결과만으로는 선거에서 무슨 일이 벌어졌는지 명백하게 증명할 수 없다.
'2020.4.15_총선' 카테고리의 다른 글
| 선거의 이상징후에 대한 통계적 탐지 가능성(Klimek, et al.) (0) | 2023.04.25 |
|---|---|
| 미베인 교수의 논문에 대한 몇가지 반론 살펴보기 (0) | 2023.04.23 |
| 선거에서 "통계적 기적"은 과연 실제로 일어나는가 (0) | 2023.04.21 |
| 총선 투표지 분류기의 외부 통신 가능성에 대한 약간의 고찰 (가짜 DNS 서버 문제) (0) | 2023.04.21 |
| 3파전 수수께끼(3) - 총선 사전투표자와 당일투표자는 서로 다른 집단인가 (0) | 2023.04.21 |

